Énoncé du problème

À partir d'un nombre de candidats qui souhaitent intégrer une association,
ainsi que d'une liste d'approbations et de désapprobations pour chaque membre actuel de cette même association, déterminez s'il existe une solution qui satisfasse au moins une des exigences de chaque membre actuel de l'association.
L'image ci-dessous donne un exemple et une illustration du problème.

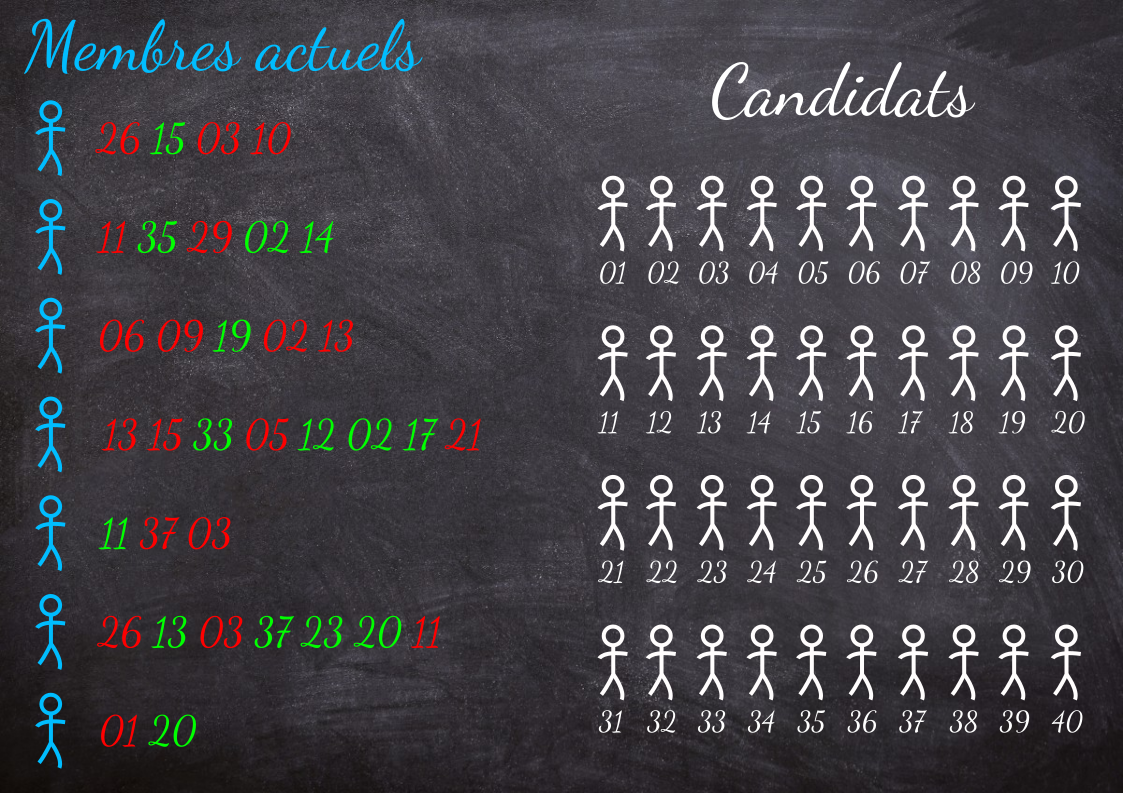
Les nombres rouges sont des désapprobations, ou bien des vétos, les nombres verts sont des approbations.
Il s'agit donc de déterminer si au moins une des exigences de chaque membre est satisfaite pour valider ou invalider le vote.

Ici nous partons du postulat O(N) ‹= N² + 2N.
O étant la lettre communément admise pour symboliser la complexité algorithmique.
N étant le nombre de valeurs à l'entrée du cœur de l'algorithme, il s'agit ici de la liste des exigences des membres.
La complexité de l'algorithme serait donc polynomiale, bien que donnant un résultat en un temps assez conséquent, en fonction de la taille en entrée du programme.

Pour N = 10, N² + 2N = 120.
Pour N = 20, N² + 2N = 440.
Pour N = 50, N² + 2N = 2 600.
Pour N = 100, N² + 2N = 10 200.
Pour N = 500, N² + 2N = 251 000.
Pour N = 1000, N² + 2N = 1 002 000.
Etc...

Le nombre d'itérations sera donc relativement vite démultiplié, mais pas de façon exponentielle, l'exposant de N étant de valeur fixe.

Si cet algorithme est correct on pourrait déterminer que P = NP, le problème SAT étant considéré comme le problème NP-complet le plus générique de toute la classe des problèmes NP-complets.
Ici nous tentons de démontrer que ce problème SAT, réputé appartenir à la classe NP-complet, peut en réalité se résoudre en un temps polynomial, et qu'il appartient donc à la classe P.
Ce qui en principe suffirait à démontrer P = NP.

D'un point de vue mathématiques prenons cet exemple :



Définition des symbôles utilisés :
: OU logique.
: ET logique.
: NON logique.
_i : Variable booléenne.

En supprimant les variables négativées ou positivées (véto(s) et approbation(s)), on obtient :



Si v2 ET v4 sont vraies, alors l'équation dans son ensemble est vraie.
Chaque groupe de parenthèses est considéré comme un membre, on peut aussi parler de "clause".
Nous sommes donc ici sur un problème 3-SAT (3 exigences par membre/clause).
Les clauses sont séparées par des ET logiques, et les exigences par des OU logiques.

L'algorithme présenté ici supprime toutes les contradictions approbations / vétos afin de déterminer s'il reste au moins une exigence satisfaite par membre.

Ceci dit cet algorithme ne permet pas de déterminer avec exactitude si une solution de succès existe ou non. Il peut passer à côté de certaines solutions de succès.

Consultez la source Javascript du programme ici : https://github.com/Kitu83/sat/blob/main/sat.js

Pour tout commentaire ou toute suggestion, vous pouvez nous écrire à l'aide du formulaire en bas de page, ou bien directement par email.

Le formulaire ci-dessous vous permet de tester l'algorithme de résolution du problème SAT.
La case à cocher "Max" vous permet de définir une valeur maximum, et donc un nombre inférieur ou égal à cette valeur sera choisi aléatoirement.